Grad Student Solves the Conway Knot, a Math Problem That Has Stumped Experts for 50 Years

The picture below may not look that complicated to people unfamiliar with knot theory, but it's been confounding mathematicians for decades. Now, a graduate student-turned-MIT professor holds the honor of being the first person to solve the Conway Knot problem in 50 years, the Boston Globe reports.

While studying at the University of Texas in 2018, Lisa Piccirillo came up with a proof of the Conway Knot in less than week. Her work was published in the journal Annals of Mathematics earlier this year, and the math world immediately took notice. On July 1, the 29-year-old started a new job as an assistant professor at MIT.

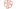
The Conway Knot is named after John Horton Conway, the English mathematician who discovered the mathematical knot half a century ago. A mathematical knot is a tangled shape that appears to be made from a single, unbroken line. Knot theory is a subcategory of topology (the study of objects' immutable geometric properties), and it examines how these shapes are possible. This theory of mathematics has real world applications in understanding things like the DNA double-helix and the shape of the universe.

The Conway Knot is one of the more notorious problems in knot theory, with a line that overlaps in 11 different places. In knot theory, some knots are "slices," which means they could be made by slicing a four-dimensional knotted sphere, and it was unclear whether the Conway Knot belonged in this category. Piccirillo devised her own knot, now called Piccirillo's knot, made out of the same four-dimensional shape, or "trace," associated with the Conway Knot. Because her knot wasn't a slice, she determined that the Conway Knot couldn't be one either.

Piccirillo graduated from the University of Texas in 2019 and took a postdoctoral position at Brandeis. While most postdoctoral jobs last three or four years, Piccirillo had only been out of grad school for 14 months when she was hired by MIT.